Category of chain complexes

In mathematics, chain complexes arise naturally in topology and geometry. For example, homology and cohomology theories all make use of chain complexes. To define a chain complex, fix an abelian category, say the category of modules over a commutative ring. Let M_i be a series of objects in this category with maps 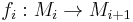such that the composition of two consecutive maps is zero. Then the collection of M_i along with the morphisms f is called a chain complex. There is a natural notion of a morphism between chain complexes called a chain map. Given two complexes M_* and N_*, a chain map between the two is a series of homomorphisms from M_i to N_j such that the entire diagram commutes. Chain complexes with chain maps form a category.